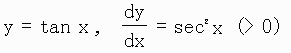
 今回は、前章に引き続きマクローリン展開の応用です。
円周率を求めてみましょう。
今回は、前章に引き続きマクローリン展開の応用です。
円周率を求めてみましょう。
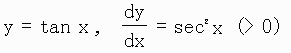
はい、そうです。では、Tan-1xの微分はどうなるでしょうか。
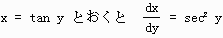
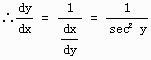
ここで、sec2y = 1 + tan2y = 1 + x2
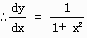
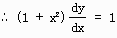
この両辺をLeibniz(ライプニッツ)の定理にあてはめ、 x=0を代入すると
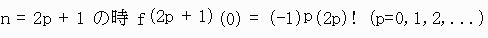
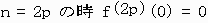
これから、tan-1をマクローリン展開すると
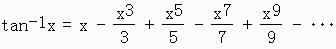
これにx=1を代入すると
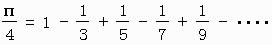
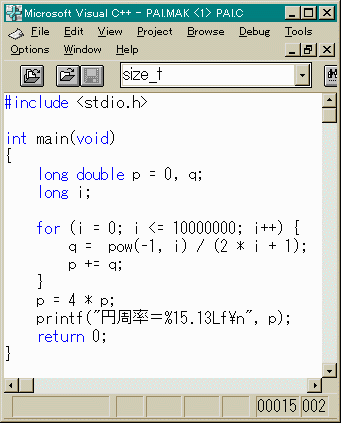 計算回数をやたら大きくしないと、なかなかいい値が
でません。これは、分数の値がなかなか小さくならず
収束しないからですね。ほんとは、もっと早く収束
させるやり方があります。たいていの参考書に
載っていますので読んでみてください。
ここでは、マクローリン展開に忠実にプログラムを
書いただけです。
計算回数をやたら大きくしないと、なかなかいい値が
でません。これは、分数の値がなかなか小さくならず
収束しないからですね。ほんとは、もっと早く収束
させるやり方があります。たいていの参考書に
載っていますので読んでみてください。
ここでは、マクローリン展開に忠実にプログラムを
書いただけです。
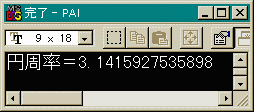 円周率は
円周率は
3.14159265358979...
ですから小数点以下6桁くらいまでしか信用できませんね。
Update Dec/22/1996 By Y.Kumei